^-^
算法
最近更新：2025-10-24   |   字数总计：5.6k   |   阅读估时：24分钟   |   阅读量：次
  1. 算法
    1. 数据结构简述
      1. 数组
      2. 栈、队列与链表
      3. 二叉树
    2. 二叉树的递归遍历
    3. 算法的复杂度衡量
    4. 前端数据操作
      1. 数组的应用
      2. 字符串的应用
    5. 链表专题
      1. 链表的应用
      2. 快慢指针与多指针
      3. 环形链表
    6. 栈与队列
    7. 遍历专题
    8. 二叉树专题
    9. 排序算法专题
    10. 动态规划专题
    11. 头部企业真题训练
    12. 其它

算法

数据结构简述

数组

  • 数组
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    // 不同的创建方式
    const arr1 = [1, 2, 3, 4];
    const arr2 = new Array(7).fill(1); // 创建一个长度为7的数组并填入1
    // 数组的访问
    arr1[0];
    // 数组的常见遍历方法
    arr.map((v, i) => {});
    for (let i = 0; i < arr1.length; i++) {
      arr1[i];
    }
    arr.forEach((v, i) => {});
  • 二维数组(矩阵)
    1
    2
    3
    4
    5
    6
    7
    8
    // 不同的创建方式
    let arr1 = [];
    for (let i = 0; i < arr1.lengh; i++) {
      arr1[i] = [];
    }
    // 使用fill生成二维数组 ❌ 存在引用类型的指向同一数据问题
    const arr2 = new Array(7).fill([]);
    arr2[0][0] = 1; // 当访问arr2时;arr2的一层值都为同一数组的索引，所以当改其中一项时，全部被修改
  • 小结
    • 二维数组是数组套数组，也就是每个元素都是数组的数组
    • 在数学中，形如长方阵列排列的复数或实数集合，被称为“矩阵”。因此二维数组的别名就叫“矩阵”
    • 当给 fill 传递一个入参时，如果这个入参的类型是引用类型，那么 fill 在填充坑位时填充的其实就是入参的引用

栈、队列与链表

  • 栈
    1
    2
    3
    4
    5
    6
    7
    8
    9
    const stack = new Array();
    // 入栈
    stack.push("货物A");
    stack.push("货物B");
    stack.push("货物C");
    while (stack.length > 0) {
      stack.pop(); // 出栈
      console.log(stack[stack.length - 1] + " 已卖出");
    }
  • 队列
    1
    2
    3
    4
    5
    6
    7
    8
    9
    // 只允许从尾部添加元素,只允许从头部添加元素
    const queue = [];
    queue.push("顾客 1");
    queue.push("顾客 2");
    queue.push("顾客 3");
    while (queue.length > 0) {
      queue.shift();
      console.log(queue[0] + " 已取餐");
    }
  • 链表
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    /* 链表元素的新增操作 */
    function ListNode(val = null) {
      this.val = val;
      this.next = null;
    }
    const node1 = new ListNode(1);
    const node2 = new ListNode(2);
    const node3 = new ListNode(3);
    node1.next = node2;
    node2.next = node3; // 将结点建立连接
    /* 链表元素的插入操作 */
    const nodeT = new ListNode(1.5);
    nodeT.next = node1.next;
    node1.next = nodeT; // 将nodeT 插入node1 和 node2 之间
    /* 链表元素的删除操作 */
    node1.next = nodeT.next; // 删除了nodeT
    /* 链表的遍历与访问操作 */
    let current = node1;
    while (current !== null) {
      console.log("当前遍历到元素" + current.val);
      current = head.next;
    }
  • 小结
    • 栈是一种先进后出的数据结构(只用 pop 和 push 完成增删的“数组”)
    • 栈的两个特征 1. 只允许从尾部添加元素 2. 只允许从尾部取出元素
    • 队列是一种先进先出的数据结构(只用 push 和 shift 完成增删的“数组”)
    • 队列的两个特征 1. 只允许从尾部添加元素 2. 只允许从尾头部取出元素
    • 链表和数组相似，它们都是有序的列表、都是线性结构（有且仅有一个前驱、有且仅有一个后继）不同点在于，链表中，数据单位的名称叫做“结点”，而结点和结点的分布，在内存中可以是离散的.
    • 链表的插入在于插入的节点去承接前驱节点的 next 指针,然后前驱节点的 next 指针再等于插入节点即可,防止直接将前驱节点的 next 指向插入节点的操作时出现断层
    • 链表删除的标准是：在链表的遍历过程中，无法再遍历到某个结点的存在。按照这个标准，要想遍历不到 node3，我们直接让它的前驱结点的 next 指针跳过它、指向后驱的后继即可
    • 链表的插入/删除效率高，但访问效率低，数组的访问效率高，但插入效率低
    • 在 js 中如果生成一个纯数组如:[1,2,3,4],它对应的是连续内存，但是如果是不同类型的元素的数组如：[‘haha’,1,{a:1}]，那么此时 Js 的底层将使用哈希映射分配内存空间，由对象链表来实现。此时它的内存便不再是连续的
    • 有时会设定一个 head 指针来专门指向链表的开始位置,不过是非必须的

二叉树

  • 示例

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    // 二叉树的创建
    function TreeNode(val = null) {
      this.val = val;
      this.left = this.right = null;
    }
    const baseNode = new TreeNode("1"); // 根部节点

    const leftSecNode = new TreeNode("2-l"); // 根部节点
    const rightSecNode = new TreeNode("2-r"); // 根部节点

    const thirdNode1 = new TreeNode("2-l"); // 根部节点
    const thirdNode2 = new TreeNode("2-l"); // 根部节点
    const thirdNode3 = new TreeNode("2-l"); // 根部节点
    const thirdNode4 = new TreeNode("2-l"); // 根部节点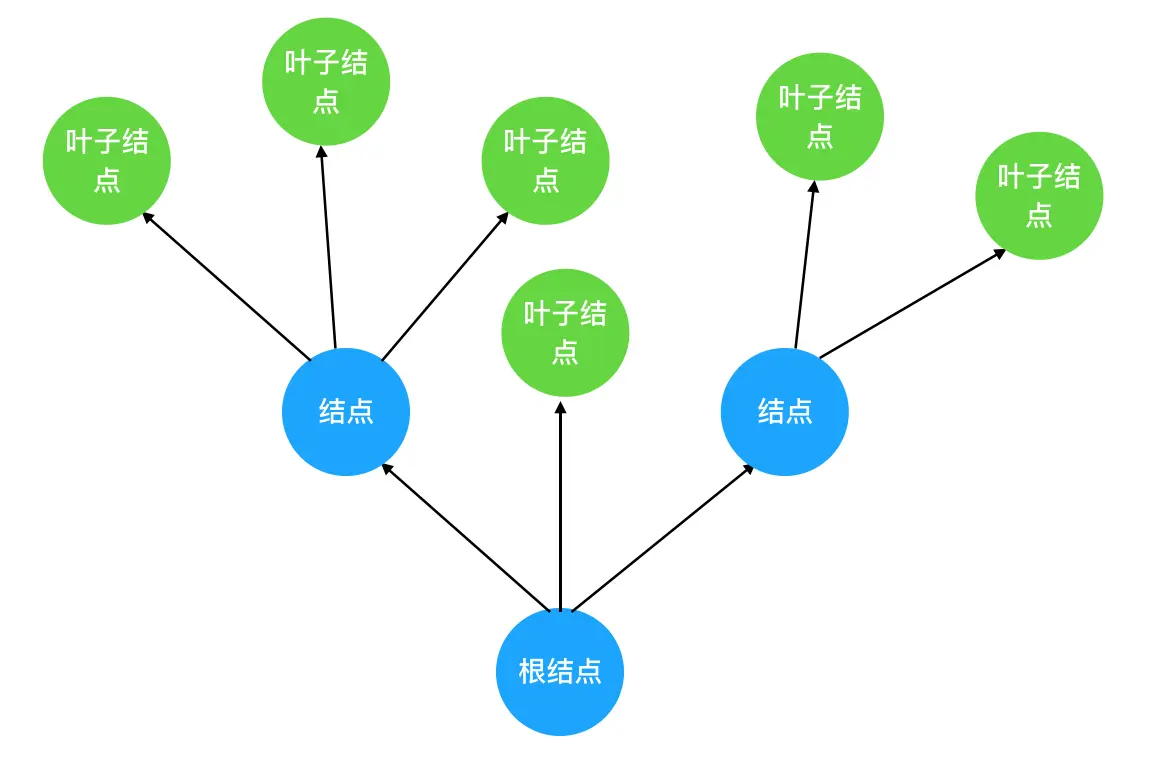

  • 小结

    • 树的关键特性和重点概念
      • 树的层次计算规则：根结点所在的那一层记为第一层，其子结点所在的就是第二层，以此类推
      • 结点和树的“高度”计算规则：叶子结点高度记为 1，每向上一层高度就加 1，逐层向上累加至目标结点时，所得到的的值就是目标结点的高度。树中结点的最大高度，称为“树的高度”。
      • “度”的概念：一个结点开叉出去多少个子树，被记为结点的“度”。比如我们上图中，根结点的“度”就是 3。
      • “叶子结点”：叶子结点就是度为 0 的结点。在上图中，最后一层的结点的度全部为 0，所以这一层的结点都是叶子结点。
    • 二叉树：
      • 每个节点最多有两个子节点，分别称为左子节点和右子节点
      • 二叉树可以没有根节点，作为一颗空树存在；否则，它由根节点和左子树以及右子树连结，且左子树和右子树都是二叉树，并且左右子树的位置是严格约定、不能交换的
      • 满二叉树：每一个分支都是满的的二叉树
      • 完全二叉树：只需保证最后一个节点之前的节点都齐全的二叉树

二叉树的递归遍历

  • 递归遍历
    • 二叉树数据结构
      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      // 遍历数据模板
      const temp_tree = {
        val: "A",
        left: {
          val: "B",
          left: { val: "D", right: null, left: null },
          right: { val: "E", right: null, left: null },
        },
        right: {
          val: "C",
          left: null,
          right: { val: "F", right: null, left: null },
        },
      };
    • 先序遍历
      1
      2
      3
      4
      5
      6
      7
      function preorder(treeNode) {
        if (!treeNode) return; // 递归的边界为节点为空
        console.log("当前遍历到了" + treeNode.val); // 输出节点
        preorder(treeNode.left); // 遍历左子树
        preorder(treeNode.right); // 遍历右子树
      }
      preorder(temp_tree);
    • 中序遍历
      1
      2
      3
      4
      5
      6
      7
      function inorder(treeNode) {
        if (!treeNode) return; // 递归的边界为节点为空
        inorder(treeNode.left); // 遍历左子树
        console.log("当前遍历到了" + treeNode.val);
        inorder(treeNode.right); // 遍历右子树
      }
      inorder(temp_tree);
    • 后序遍历
      1
      2
      3
      4
      5
      6
      7
      function postorder(treeNode) {
        if (!treeNode) return; // 递归的边界为节点为空
        postorder(treeNode.left); // 遍历左子树
        postorder(treeNode.right); // 遍历右子树
        console.log("当前遍历到了" + treeNode.val);
      }
      postorder(temp_tree);
  • 迭代遍历
    • 层序遍历
  • 小结
    • 递归函数：编程语言中，函数 Func(Type a,……)直接或间接调用函数本身，则该函数称为递归函数。
    • 编写一个递归函数之前，要明确两样东西：“代表每一次重复的内容是什么的递归式” 和 “代表什么时候停下来的递归边界”
    • 二叉树的遍历中，在保证“左子树一定先于右子树遍历”的情况下共有三种情况, 根据根节点所处的不同位置，从而分别对应了二叉树的先序遍历、中序遍历和后序遍历规则
      1. 根结点 -> 左子树 -> 右子树
      2. 左子树 -> 根结点 -> 右子树
      3. 左子树 -> 右子树 -> 根结点

算法的复杂度衡量

  • 时间复杂度

    时间复杂度从小到大排列

    • 常数时间 O(1)
    • 对数时间 O(logn)
    • 线性时间 O(n)
    • 线性对数时间 O(nlogn)
    • 二次时间 O(n^2)
    • 三次时间 O(n^3)
    • 指数时间 O(2^n)
  • 空间复杂度
    • 常数空间复杂度 O(1)
      1
      2
      3
      function sum(a, b) {
        return a + b;
      }
    • 线性空间复杂度 O(n)
      1
      2
      3
      4
      5
      6
      7
      function createArray(n) {
        let arr = [];
        for (let i = 0; i < n; i++) {
          arr.push(i);
        }
        return arr;
      }
    • 平方空间复杂度 O(n^2)
      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      function createMatrix(n) {
        let matrix = [];
        for (let i = 0; i < n; i++) {
          let row = [];
          for (let j = 0; j < n; j++) {
            row.push(0);
          }
          matrix.push(row);
        }
        return matrix;
      }
  • 小结
    • 时间复杂度，它反映的不是算法的逻辑代码到底被执行了多少次，而是随着输入规模的增大，算法对应的执行总次数的一个变化趋势
    • 空间复杂度是对一个算法在运行过程中临时占用存储空间大小的量度。它是内存增长的趋势。

前端数据操作

数组的应用

  • 两数求和问题 (map 映射)

    题目：给定一个整数数组 nums 和一个目标值 target，请你在该数组中找出和为目标值的那 两个 整数，并返回他们的数组下标。
    示例：给定 nums = [2, 7, 11, 15], target = 9 输出: [0, 1]
    思路：

    1
    2
    3
    4
    5
    6
    7
    8
    // 简单粗暴法
    function twoSum(nums, target) {
      for (let i = 0; i < nums.length - 1; i++) {
        for (let j = i + 1; j < nums.length; j++) {
          if (nums[i] + nums[j] === target) return [i, j];
        }
      }
    }
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    // 空间换时间，通过映射优化算法执行时间
    function twoSum(nums, target) {
      // Map对象来建立映射
      let map = new Map();
      for (let i = 0; i < nums.length; i++) {
        let val = nums[i];
        let diff = target - val;
        if (map.has(diff)) {
          let diffIdx = map.get(diff);
          return [i, diffIdx];
        }
        map.set(val, i);
      }
    }
    function twoSum(nums, target) {
      // 对象建立映射法
      let map = {};
      for (let i = 0; i < nums.length; i++) {
        let val = nums[i];
        let diff = target - val;
        let diffIdx = map[diff];
        if (diffIdx !== undefined) {
          return [i, diffIdx];
        }
        map[val] = i;
      }
    }
  • 合并两个有序数组(双指针)

    题目：给你两个有序整数数组 nums1 和 nums2，请你将 nums2 合并到 nums1 中，使 nums1 成为一个有序数组。
    说明: 初始化 nums1 和 nums2 的元素数量分别为 m 和 n 。 你可以假设 nums1 有足够的空间（空间大小大于或等于 m + n）来保存 nums2 中的元素。
    示例：nums1 = [1,2,3], m = 3, nums2 = [2,5,6], n = 3 ; 输出: [1,2,2,3,5,6]
    思路：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    function merge(nums1, m, nums2, n) {
      let i = m - 1; // nums1 指针下标
      let j = n - 1; // nums2 指针下标
      let k = m + n - 1; // nums1 总长度下标
      while (i >= 0 && j >= 0) {
        if (nums1[i] >= nums2[j]) {
          nums1[k] = nums1[i];
          i--;
          k--;
        } else {
          nums1[k] = nums2[j];
          j--;
          k--;
        }
      }
      while (j >= 0) {
        nums1[k] = nums2[j];
        j--;
        k--;
      }
      return nums1;
    }
  • 三数求和问题(对撞指针)

    题目：给你一个包含 n 个整数的数组 nums，判断 nums 中是否存在三个元素 a，b，c ，使得 a + b + c = 0 ?请你找出所有满足条件且不重复的三元组。
    示例： 给定数组 nums = [-1, 0, 1, 2, -1, -4], 满足要求的三元组集合为: [ [-1, 0, 1], [-1, -1, 2] ]
    思路：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    const threeSum = function (nums) {
      let res = [];
      nums = nums.sort((a, b) => a - b); // 使用双指针的前提是有序
      for (let i = 0; i < nums.length - 2; i++) {
        // -2 是因为两个指针的位置会占用到这个位置
        let lp = i + 1; // 左指针
        let rp = nums.length - 1; // 右指针
        if (i > 0 && nums[i] === nums[i - 1]) continue; // 如果当前元素和之前元素重复则证明
        while (lp < rp) {
          const sum = nums[i] + nums[lp] + nums[rp];
          if (sum < 0) {
            // 证明左指针小了, 向右移动
            lp++;
            while (lp < rp && nums[lp] === nums[lp + 1]) lp++; // 左指针向右移动时,左指针的右一个元素重复时，再向右移动一次
          }
          if (sum > 0) {
            // 证明右指针大了, 向左移动
            rp--;
            while (lp < rp && nums[rp] === nums[rp - 1]) rp--; // 右指针向左移动时,右指针的左一个元素重复时，再向左移动一次
          }
          if (sum == 0) {
            // 当结果值等于0, 左右指针需要同时过一格
            res.push([nums[i], nums[lp], nums[rp]]);
            lp++;
            rp--;
            while (lp < rp && nums[lp] === nums[lp + 1]) lp++;
            while (lp < rp && nums[rp] === nums[rp - 1]) rp--;
          }
        }
      }
      return res;
    };
    threeSum([2, -1, 2, 1, 3, -2, 0, 1, 4, 3]);
  • 小结
    • 几乎所有的求和问题，都可以转化为求差问题
    • 当发现自己的代码里有两层循环时，先反思一下，能不能用空间换时间，把它优化成一层循环
    • 双指针法用在涉及求和、比大小类的数组题目里时，大前提往往是：该数组必须有序。否则双指针根本无法帮助我们缩小定位的范围
    • 当遇到两个关键字——“有序”和“数组”时，立刻把双指针法调度进你的大脑内存。普通双指针走不通，立刻想对撞指针

字符串的应用

  • 反转字符串

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    // 反转字符串(可用于判断是否回文字符串)
    const str = "abcd";
    const str2 = str.split("").reverse().join(""); // 输出dcba
    let isReveice = str === str2 ? true : false;
    // 判断一个字符串是否是回文字符串
    function isPalindrome(str) {
      let strArr = str.split("");
      for (let i = 0; i < strArr.length; i++) {
        const idx = i;
        const len = strArr.length - 1 - i;
        if (len > idx && strArr[idx] !== strArr[len]) return false;
      }
      return true;
    }

  • 回文字符串的衍生问题

    真题描述：给定一个非空字符串 s，最多删除一个字符。判断是否能成为回文字符串。
    示例 1: 输入: “aba” 输出: True 。示例 2:输入: “abca” 输出: True
    思路：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    const validPalindrome = function (str) {
      let sp = 0; // 起始指针
      let ep = str.length - 1; // 末尾指针
      while (sp < ep && str[sp] === str[ep]) {
        sp++;
        ep--;
      }
      if (isPalindrome(str, sp + 1, ep)) {
        // 左指针右移一位是否对此
        return true;
      }
      if (isPalindrome(str, sp, ep - 1)) {
        // 右指针左移一位判断是否对称
        return true;
      }
      function isPalindrome(str, sp, ep) {
        while (sp < ep) {
          if (str[sp] !== str[ep]) {
            return false;
          }
          sp++;
          ep--;
        }
        return true;
      }
      return false; // 默认返回false
    };
    // 回文字符串：从中间位置“劈开”，两边的两个子串在内容上是完全对称的字符串

  • 字符串匹配问题

    真题描述：设计一个支持以下两种操作的数据结构：void addWord(word) bool search(word) search(word) 可以搜索文字或正则表达式字符串，字符串只包含字母 . 或 a-z 。”. 可以表示任何一个字母。”

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    const WordDictionary = function () {
      this.word = {};
    };
    WordDictionary.prototype.addWord = function (word) {
      const len = word.length;
      if (!this.word[len]) {
        this.word[len] = [];
      }
      this.word[len].push(word);
    };
    WordDictionary.prototype.search = function (word) {
      const len = word.length;
      if (!word.includes(".")) {
        return this.word[len].includes(word);
      } else {
        let reg = new RegExp(word);
        return this.word[len].some((item) => reg.test(item));
      }
      return false;
    };
    const wordT = new WordDictionary();
    wordT.addWord("bad");
    wordT.addWord("dad");
    wordT.addWord("mad");
    console.log(wordT.search("pad"));
    console.log(wordT.search("bad"));
    console.log(wordT.search(".ad"));
    console.log(wordT.search("b.."));

  • 字符串与数字之间的转换问题

    思路：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    const myAtoi = function (str) {
      // 正则中()代表捕获组：捕获组可以将匹配的子字符串捕获并存储起来，以便在之后的操作中使用
      const reg = /\s*([-\+]?[0-9]*).*/;
      const groups = str.match(reg);
      const max = Math.pow(2, 31) - 1;
      const min = -max - 1;

      let targetNum = 0;
      if (groups) {
        targetNum = +groups[1];
        if (isNaN(targetNum)) {
          // 不能进行有效的转换时，请返回 0
          targetNum = 0;
        }
      }

      if (targetNum > max) {
        return max;
      } else if (targetNum < min) {
        return min;
      }

      return targetNum;
    };

链表专题

处理链表的本质，是处理链表结点之间的指针关系

链表的应用

  • 链表的合并
    • 题目：将两个有序链表合并为一个新的有序链表并返回。新链表是通过拼接给定的两个链表的所有结点组成的。 【考察链表结点之间的处理关系】
    • 示例: 输入 1->2->4, 1->3->4 输出 1->1->2->3->4->4
    • 思路: 新建链表,然后循环判断 2 个有序链表的大小,谁大就链接到新链表中,并将该条链表的指向向前走一步
    • 解法：
      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      16
      17
      18
      19
      20
      21
      22
      23
      24
      25
      26
      27
      28
      29
      30
      31
      32
      33
      34
      35
      36
      37
      38
      39
      40
      41
      // 创建ListCode单节点
      function ListNode(val: number | string | null = null) {
        this.node = val;
        this.next = null;
      }
      interface ListNode {
        node: number | string | null;
        next: ListNode | null;
      }
      // 创建ListCode
      function createListNode(data: Array<number | string>) {
        const head = new ListNode();
        let cur = head;
        for (let i = 0; i < data.length; i++) {
          cur.node = data[i];
          cur.next = i === data.length - 1 ? null : new ListNode();
          cur = cur.next;
        }
        return head;
      }
      let l1 = createListNode([3, 4, 5]);
      let l2 = createListNode([1, 2, 3, 6, 7]);
      function mergeList() {
        let cur;
        let head = new ListNode();
        cur = head;
        while (l1 && l2) {
          if (l1.node <= l2.node) {
            cur.next = l1;
            l1 = l1.next;
            cur = cur.next;
          } else {
            cur.next = l2;
            l2 = l2.next;
            cur = cur.next;
          }
        }
        cur.next = l1 === null ? l2 : l1;
        return head.next;
      }
      console.log(mergeList(l1, l2));
  • 链表的去重（保留一位重复元素）
    • 题目：给定一个排序链表，删除所有重复的元素，使得每个元素只出现一次。【考察链表的删除操作】
    • 示例：输入: 1->1->2->3->3 输出: 1->2->3
    • 思路：链表的删除操作是让目标节点的前驱节点 next 等于(指向)后驱节点即可
    • 解法：
      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      function deleteDuplicates(head) {
        let cur = head;
        while (cur && cur.next) {
          if (cur.node === cur.next.node) {
            cur.next = cur.next.next;
          } else {
            cur = cur.next;
          }
        }
        return head;
      }
  • 链表的去重 (删除所有重复元素)
    • 题目：给定一个排序链表，删除所有含有重复数字的结点，只保留原始链表中 没有重复出现的数字。【考察当前节点的删除：dummy 节点的使用】
    • 示例: 输入: 1->1->1->2->3 输出: 2->3
    • 思路：通过引入 dummy 节点并指向链表后,通过遍历来确认 后驱节点 及 后驱节点的后驱节点是否相等，如果相等，则记录下相等的值，然后遍历后驱节点如果等于该值便删除
    • 解法：
      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      16
      17
      18
      19
      function deepDeleteDuplicates(head) {
        if (!head || !head.next) return;
        let dummy = new ListNode();
        dummy.next = head;
        let cur = dummy;
        // 从第二个节点开始
        while (cur.next && cur.next.next) {
          if (cur.next.node === cur.next.next.node) {
            let val = cur.next.node;
            // 记住当前的值后，删除后一位，继续并判断一下位是否重复
            while (cur.next && cur.next.node == val) {
              cur.next = cur.next.next;
            }
          } else {
            cur = cur.next; // 遍历下一位
          }
        }
        return head;
      }

快慢指针与多指针

  • 快慢指针

    • 真题描述：给定一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。【考察快慢指针的使用】

    • 示例： 给定一个链表: 1->2->3->4->5, 和 n = 2. 当删除了倒数第二个结点后，链表变为 1->2->3->5. 说明： 给定的 n 保证是有效的。

    • 思路：通过快慢指针，省略一次循环，直接可以删除从后往前数 n 的节点，初始化 dummy 节点，链接 head，新建两个快慢指针让他们都置于起始位置，然后快指针先走 n 步后，慢指针也开始走，当快指针走到最后一位，那么慢指针恰好停留的就是倒数的 n 的位置，这个时候执行删除下一位的操作即可

    • 解法：

      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      16
      17
      18
      19
      function delDetalNode(head, n) {
        let dummy = new ListNode();
        dummy.next = head;
        let slow = dummy;
        let fast = dummy;
        // fast 先走n步
        while (n > 0) {
          fast = fast.next;
          n--;
        }
        while (fast.next) {
          fast = fast.next;
          slow = slow.next;
        }
        // 执行删除操作
        slow.next = slow.next.next;

        return dummy.next;
      }

  • 完全反转链表（多指针法）

    • 真题描述：定义一个函数，输入一个链表的头结点，反转该链表并输出反转后链表的头结点。【考察多指针的使用】

    • 示例：输入: 1->2->3->4->5->NULL 输出: 5->4->3->2->1->NULL

    • 思路：只需要把每个节点的 next 指向反向即可，通过确定三个指针 pre cur next(next 指针用于保留 cur 后继节点),cur 的 next 指向 pre,然后让 pre 等于 cur,cur 等于 next

    • 解法：

      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      function reverseListNode(head) {
        let pre = null;
        let cur = head;
        while (cur) {
          let next = cur.next;
          cur.next = pre;
          pre = cur;
          cur = next;
        }

        return pre;
      }

  • 局部反转链表（）

    • 真题描述：反转从位置 m 到 n 的链表。请使用一趟扫描完成反转。【考察多指针的使用及节点前驱节点及后驱节点的指针关系】
    • 示例：输入: 1->2->3->4->5->NULL, m = 2, n = 4 输出: 1->4->3->2->5->NULL
    • 思路：在上一题的基础上，需要理解反转后的节点的前置和后驱节点的位置并保存状态。声明一个 p 节点，让 p 节点位于该截取节点的前一位，然后标记一个 leftStatus 节点，让其等于 p。那么开始的节点声明为 start 为 p 的 next 节点，pre 则为 start 节点，cur 节点则为 pre 的 next。遍历 m 到 n 的位置，让每一个 cur 的指向改变为 pre，最后，cur 会到最后一位，pre 在最后一位的前一位，那么保存的 start 节点是反转后 cur 的前驱节点，leftStatus 则是 pre 的前驱节点
    • 解法：
      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      16
      17
      18
      19
      20
      21
      22
      23
      function partReverseList(head, m, n) {
        let pre, cur, leftStatus;
        let dummy = new ListNode();
        dummy.next = head;
        let p = dummy;
        // 找到前驱节点
        for (let i = 0; i < m - 1; i++) {
          p = p.next;
        }
        leftStatus = p; // 找到左侧前驱节点
        let start = leftStatus.next; // 记录起始节点
        pre = start;
        cur = pre.next;
        for (let i = m; i < n; i++) {
          let next = cur.next;
          cur.next = pre;
          pre = cur;
          cur = next;
        }
        leftStatus.next = pre;
        start.next = cur;
        return dummy.next;
      }

环形链表

  • 判断链表是否成环
    • 真题描述：给定一个链表，判断链表中是否有环。
    • 示例： 输入：[3,2,0,4]（链表结构如下图） 输出：true 解释：链表中存在一个环
    • 思路：
    • 解法：
  • 定位环的起点
    • 真题描述：给定一个链表，返回链表开始入环的第一个结点。 如果链表无环，则返回 null。
    • 示例： 输入：head = [3,2,0,-4]（如下图） 输出：tail connects to node index 1 解释：链表中有一个环，其尾部连接到第二个结点。
    • 思路：
    • 解法：

栈与队列

遍历专题

二叉树专题

排序算法专题

动态规划专题

头部企业真题训练

其它

  • 算法面试评价逻辑
2024-02-10 该篇文章被 安德鲁 归为分类: 笔记

上一篇：设计模式 下一篇：工作经验总结
永远相信美好的事情即将发生